Polarization reduction by minimum-cardinality edge additions
Complexity and integer programming approaches
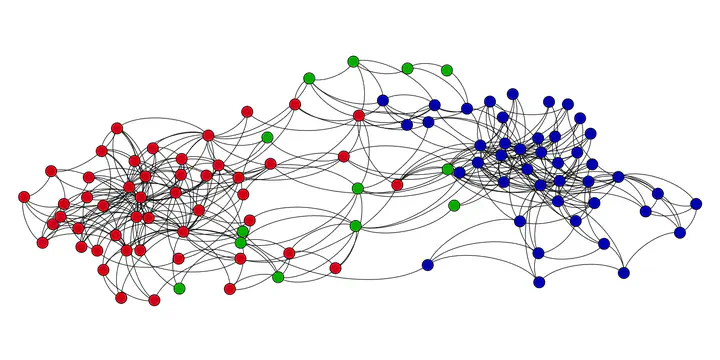 Network of books about U.S. politics sold by Amazon.com. Red, green, and blue vertices represent, respectively, conservative, neutral, and liberal books.
Network of books about U.S. politics sold by Amazon.com. Red, green, and blue vertices represent, respectively, conservative, neutral, and liberal books.Abstract
Real-world networks are often extremely polarized because the communication between different groups of vertices can be weak and, most of the time, only vertices within the same group or sharing the same beliefs communicate to each other. In this work, we introduce the minimum-cardinality edge addition problem (MinCEAP) as a strategy for reducing polarization in real-world networks based on the principle of minimum external interventions. We present the problem formulation and discuss its complexity, showing that its decision version is NP-complete. We also propose three integer programming formulations for the problem and discuss computational results on artificially generated and real-life instances. Randomly generated instances with up to 1000 vertices are solved to optimality. In real-life instances, we show that polarization can be reduced to the desired threshold with the addition of a few edges. The minimum intervention principle and the methods developed in this work are shown to constitute an effective strategy for tackling polarization issues in practice in social, interaction, and communication networks, which is a relevant problem in a world characterized by extreme political and ideological polarization.